
Based on the measurement of an angle, they are divided into four types: We represent an angle by the symbol ∠.Īn angle involves two legs and one common vertex at which two lines meet.įor example, ∠AOD is formed when lines AB and CD intersect with each other.Īlso, ∠AOD is formed between the leg AO and OD, so we include A, O, and D while naming the angle.ĭo you know that the position of leg points does not matter as long as the common vertex is the middle letter in the angle name Measurement of an AngleĪn angle can measure from zero (0) degrees to 360 degrees. We are the most reviewed online GMAT Prep company with 2500+ reviews on GMATClub, as of March 2023.Īn angle is formed when two lines intersect each other.
#Appropriate names for a line geometry trial
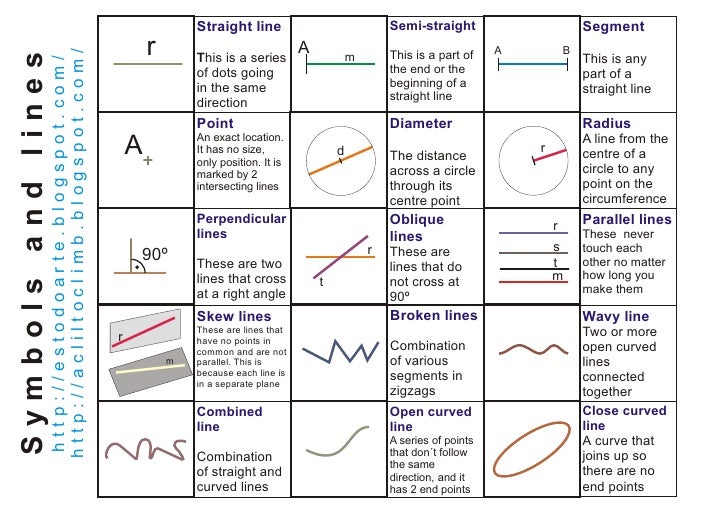
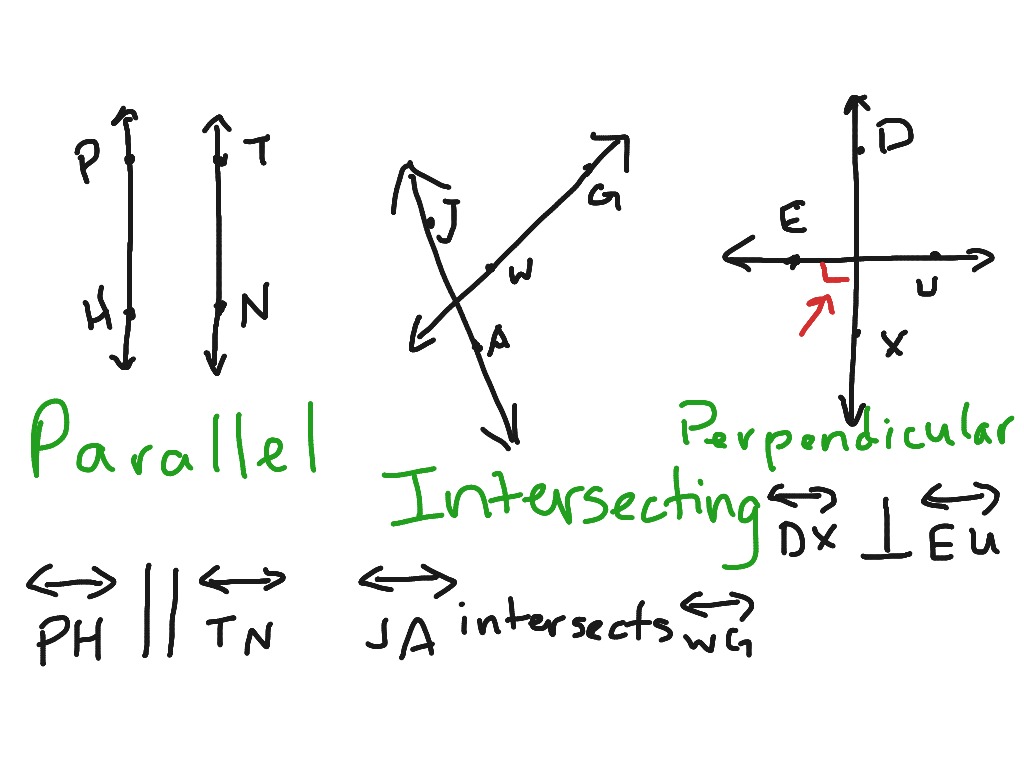
Join the world’s most successful prep company for a free trial and see the difference it can make. Watch this video to know more:Īre you struggling with GMAT quant? e-GMAT provides structured learning from foundations to help you master the skills needed for a high score. Our xPERT not only curates the most optimized learning path but also tracks your improvement, ensuring that you get to your target Quant score quickly and reliably. Start your journey of getting a Q50-51 on the GMAT with e-GMAT’s AI-driven online preparation course. Scoring a Q50-51 on the GMAT helps you get a 700+ GMAT score. Next, we take a look at angles and their properties. Transversal LineĪ transversal line cuts two or more lines at distinct points.įor example, Line L 3 is the transversal line in the below diagram. Two lines are intersecting lines if they meet each other at a common point.įor example, L 1 and L 2 are intersecting lines in the below diagram Parallel LinesĪ pair of lines are parallel if they never intersect.įor example, L 1, L 2, and L 3 are parallel lines in the below diagram. In a plane, there can be many lines or line segments.Īnd, these lines can be divided into a few types based on the relative positioning of a line with another line. Definition of a Line SegmentĪ line segment is a segment of a line, or in other words, we can say that a line segment is a line with two endpoints.įor example, The diagram shows a line L and one segment of this line is AB. To be the names, but it can be otherwise, so just pay attention.A line does not have any endpoints. Nothing sacred about the horizontal coordinate being called ‘$x$’ and $(x_1,y_1), (x_2,y_2)$ is that possibly irritating expression whichĪnd now is maybe a good time to point out that there is Point-slope form, since the slope $m$ of a line through two points Of course, the two-point form can be derived from the Instead, theĭescription of a vertical line through a point with horizontal Vertically, and the line can't be written that way. unless $x_1=x_2$, in which case the two points are aligned
(x_2,y_2)$ can be written (in so-called two-point form) as The equation of the line passing through two points $(x_1,y_1),.The equation of a line passing through a point $(x_o,y_o)$ andĬan be written (in so-called point-slope form).Slope of a line is rise over run, meaning vertical change divided by horizontal change (moving from left to.Phrase ‘The set of points $(x,y)$ so that’ is omitted. Still, very often the language is shortened so that the And conceivably the $x,y$ mightīe being used for something other than horizontal and verticalĬoordinates. It is not strictly correct to say that $x^2+y^2=1$ is a circle, mostly because an equation is not a circle, even The set of points $(x,y)$ so that $x^2+y^2=1$ is a Here: for example, a correct assertion is It is important to be a little careful with use of language The next idea is that an equation can describe aĬurve. Purposes as well, so don't rely on this labelling! Often the horizontal coordinate is called the x-coordinate, and often the vertical coordinate is called the y-coordinate, but the letters $x,y$ can be used for many other The old-fashioned names abscissa and ordinate The horizontal coordinate and the second is the verticalĬoordinate. (and negative means go down instead of up). The two numbers tells how far up from the origin the point is (and negative means go left instead of right), and the second of To the right horizontally the point is from the origin The second step is that points are described by ordered pairs of numbers: the first of the two numbers tells how far This is indeed usually only implicit, so we don't worry about it.

Implicitly, we need to choose a unit of measure for distances, but Origin, from which we'll measure everything else. The first thing is that we have to pick a special point, the Of geometric objects by numbers and by algebra. Let's review some basic analytic geometry: this is description


 0 kommentar(er)
0 kommentar(er)
